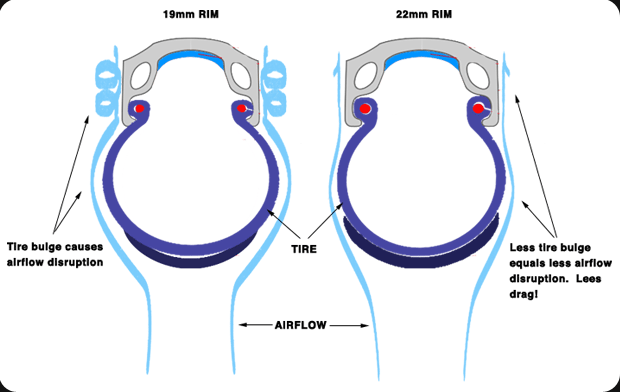
- Makes the rim stiffer and stronger
- Flattens the profile of the tire giving you a better surface contact patch
- Increases the tire volume, meaning you can run lower pressures
- Smooths the airflow between the tire and rim giving a more aerodynamic profile
Or in a single picture it does this:
So in general this is everything you could really want a rim to be and with no real disadvantages.
Except for one: I'm pretty heavy. Not fat mind you. Just heavy for a cyclist. Once you add up me, my bike and the backpack with a laptop, clothes and lunch, I can easily hit 265 lbs on my wheels. Which by the best and most scientific guide I've found means I would need to run 23mm tires at 170psi on the rear. If I rode a 23mm rim I could run 10% lower pressure, but that's still up at 153psi on the rear. And the challenge is that most tires are only rated up to 120psi, so I have a problem.
Because I'm heavier, I have to go for a wider tire.
- The best option is really a 25mm tire.
These tend to not have too much of a weight penalty over a 23mm tire, but can still take higher pressures (~120psi). The downside of a 25mm is that I'm still on the cusp of needing too much pressure (140psi, or 125psi on the 23mm rim) - The other option is a 28mm tire.
These tend to have a fairly large weight penalty though. Few manufacturers make their best tires in this width. And once you get to this width the max pressure typically drops to <100psi. For a guy of my weight I need 115psi on this tire, and I've been fortunate to have found 2 or 3 tires that can handle that and it's what I ride now.
So why don't I just get a 25mm rim for a 25mm tire and similar for a 28mm tire and rim?
- Brake calipers on bikes barely fit 23mm rims, so any larger isn't an option.
- Just because the scaling on one tire works well doesn't mean it will work on another.
Problem 1:
To get around problem 1 you simply have to use disc brakes instead. This opens a whole realm of wider-profile XC 29er rims. If you don't want to go disc, then you're stuck with 23mm HED C2 rims being the largest you can hope for at this point in time.
Problem 2:
That's what I hope to explore.
Problem Statement:
I want to run 25mm or 28mm tires on a rim that gives the same profile and advantages of using the 23mm tire on a HED C2 rims.
Assumptions:
- Surface area of a tire will remain constant once pressurized
- Profile of the tire will remain as round as possible regardless of how wide or small a rim is
- Bead-hooks vary in size and profile by rim. So what really creates the profile of the tire is the inside width of the rim, not the outside width.
- Aerodynamics aren't really that big of a deal for my style of riding or size, so I'm going to try to optimize for increased volume and cross section profile, not on matching flushly with the rim
- However, say I end up with a 24mm rim on a 25mm tire, that's still closer than a 19mm rim for smooth airflow, so I'll likely get some advantage.
- A standard road-rim has a 14mm inside width
- After emailing HED they informed me that the inside width of the HED C2 rim is 17.6mm
I explored 2 possible solutions:
- That the scaling of the rim is scaled linearly from the ratio of 17.6 to 23 and then apply to the 25 & 28mm tires.
- That the main goal is to keep the tire profile and surface area constant and see what rim would apply.
Solution 1:
Scale the rim linearly from the ratio of 17.6 to 23 and then apply to the 25 & 28mm tires.
For this it's rather simple:
- 17.6mm / 23mm = X mm / 25mm => (17.6/23) * 25mm = 19.1mm
- 17.6mm / 23mm = X mm / 28mm => (17.6/23) * 28mm = 21.4mm
Pros: This solution seems to very closely match existing inside widths for XC rims.
Cons: This solution seems almost too simple a solution, and after mocking up the profile it does not have the same profile as the HED C2 rim with a 23mm tire.
Additional details. After using SketchUp, I was able to find the following info:
23mm Tire on 17.6mm Rim:
(In parenthesis indicates dimensions for same size tire on a 14mm rim)
- Surface: 57mm (same)
- Maximum Diameter: 24.3mm (23mm)
- Cross-Sectional Area: 408.4mm² (388.0 mm²)
- Pressure vs. 14mm Rim: 95%
25mm Tire on 19.1mm Rim:
(In parenthesis indicates dimensions for same size tire on a 14mm rim)
- Surface: 68.3mm (same)
- Maximum Diameter: 28.4mm (25mm)
- Cross-Sectional Area: 572.2mm² (464.5 mm²)
- Pressure vs. 14mm Rim: 81%
28mm Tire on 21.4mm Rim:
(In parenthesis indicates dimensions for same size tire on a 14mm rim)
- Surface: 73.3mm (same)
- Maximum Diameter: 30.8mm (28mm)
- Cross-Sectional Area: 668.1mm² (592.2 mm²)
- Pressure vs. 14mm Rim: 89%
Solution 2:
To help myself better visualize everything I mocked up a 23mm tire on a 14mm rim and a 23mm tire on a 17.6mm rim.
Finding of Note: I found is that if you put a 23mm tire on a 17.6mm rim that from the center of the tire to the edge of the rim was a 45 degree angle. This symmetry seemed more than just coincidental.
I used that symmetry to come up with the following equation to simplify things. 45 degrees to each rim meant there was 90 degrees of of 360 degrees taken by the rim and 3/4 of the circle taken by the tire.
- Max Diameter of Tire * Pi * 3/4 = Cross-Sectional Surface of Tire
Unknown in this equation is Max Diameter of Tire, so solve for this:
- 25mm: 68.3mm / (3.14 * 3/4) = 29.0mm
- 28mm: 73.3mm / (3.14 * 3/4) = 31.1mm
Make circles with those dimensions, then make a line from -45 degrees on the circle to +45 degrees on the circle and you find the following optimum rim dimensions:
25mm Tire on 20.5mm Rim:
(In parenthesis indicates dimensions for same size tire on a 14mm rim)
- Surface: 68.3mm (same)
- Maximum Diameter: 29.0mm (25mm)
- Cross-Sectional Area: 594.9mm² (464.5 mm²)
- Pressure vs. 14mm Rim: 78%
28mm Tire on 22.0mm Rim:
(In parenthesis indicates dimensions for same size tire on a 14mm rim)
- Surface: 73.3mm (same)
- Maximum Diameter: 31.1mm (28mm)
- Cross-Sectional Area: 684.6mm² (592.2 mm²)
- Pressure vs. 14mm Rim: 86%
Conclusion:
It appears that Solution 1 would produced more conservative values than Solution 2; however, I believe (at least mathematically) that Solution 2 is the more optimum of the two possibilities.
- 25mm tires should be on 19.1mm to 20.5mm rims
- 28mm tires should be on 21.4mm to 22.0mm rims
One other point of note is that 25mm tires seem to gain proportionally more cross-sectional area than either 23mm or 28mm. I would have thought that things just got linearly more and more in favor of the large-diameter tires. If I had time I'd try to create a mathematical model and see where the actual minimum is. However, seeing that I can reduce tire pressure on a 25mm tire by 19-22% is a really big deal for me. That means I can instead of run a lighter stronger and generally better 25mm tire with the same lower pressure that I can run on 28mm tires in a normal setup. This actually exceeds my expectations and makes me quite excited.
What Now?
Finding the inside widths of rims is actually surprisingly hard. Some manufacturers like Mavic say it in the name (TN719 is 19mm inside), but others don't tell you unless you ask directly or do a lot of searching. Trying to find something as specific as 20.5 will likely be very difficult, so I'll just do my best to find something in the desired range. I'll likely end up with either something that says it's 21mm, but is really a little less, or something that's 19mm, and be glad I'm at least way better off than if I was on a 14mm rim.
Real-World vs. Theoretical-World
I want to see if I can get a bike shop to loan me or let me try mounting a tire on a rim of that width. This should allow me to see if things really work. But finding a shop that A) Would let me do that and B) Wouldn't just say, "You can't do that, the specs say it doesn't work."; is going to be really hard to do. Fortunately I know a few bike shop guys that I think are willing to put rules aside for some experimentation so hopefully I'll be able to report back with some results soon.